バブルソート実装・詳しい計算量解説

バブルソート(Bubble Sort)

バブルは泡の意味で、ソートしているデータが泡のように浮かび上がっていく様子に由来しています。

このサイトでのバブルソートの定義は以下の通りです。¹

計算量 $O(N^2)$

バブルソートのアルゴリズム

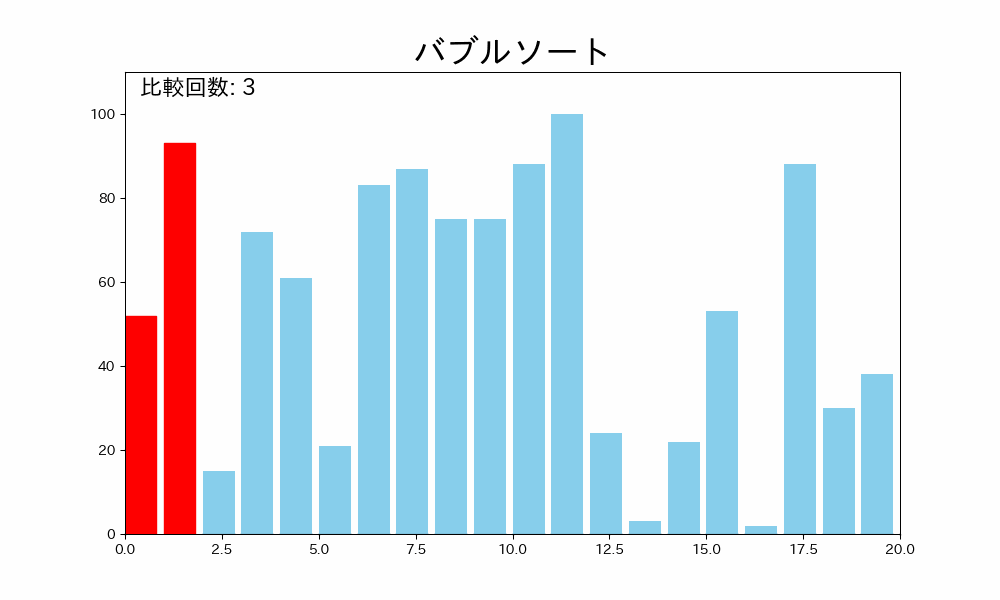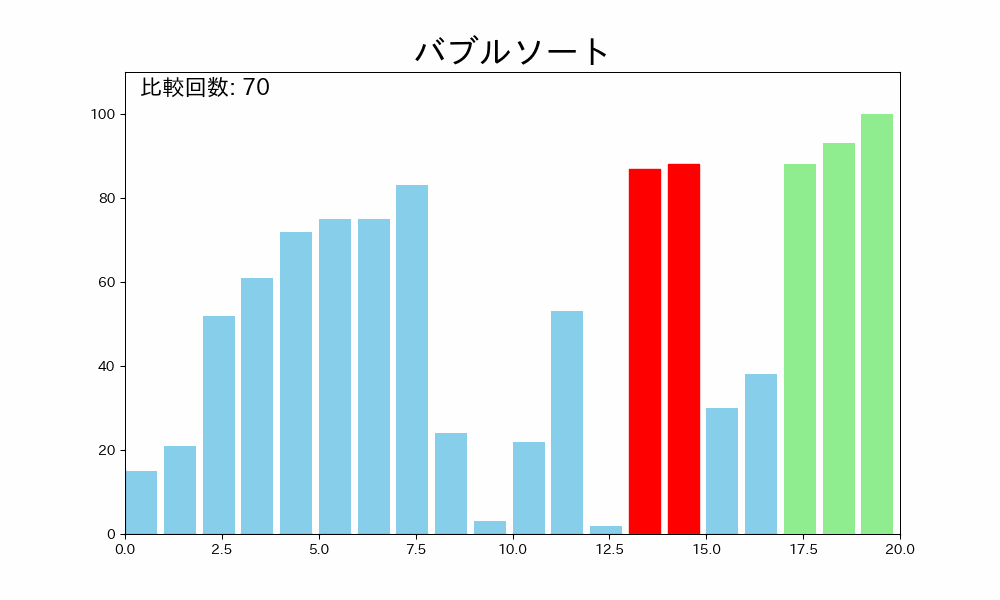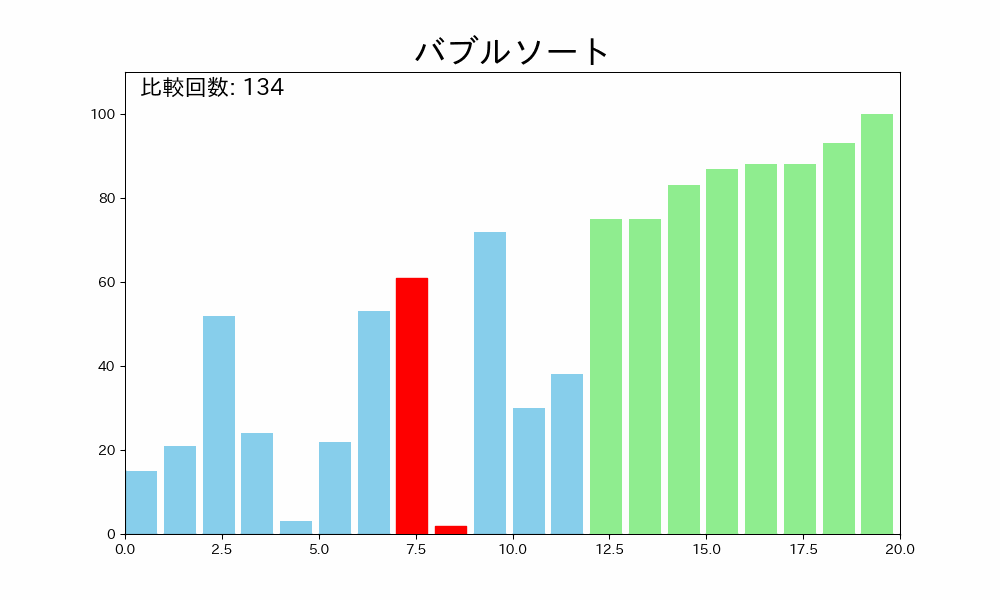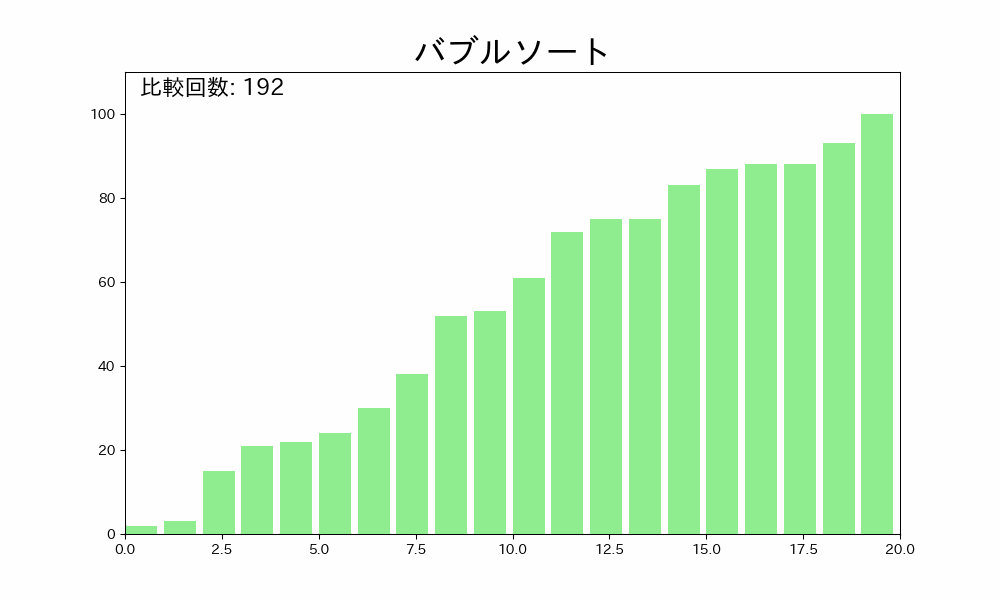
バブルソートはデータ配列のはじめから終わりまで隣接する要素を比較して、順番が逆であれば交換するという操作を繰り返し、終わりまで繰り返したら一番最後のデータをソート済みにし、再度繰り返すアルゴリズムです。

バブルソートは一番簡単と言われるソートアルゴリズムです。

詳しく手順を説明すると以下の通りです。

1. データ配列のソートされていない部分のはじめから終わりまで隣接する要素を比較する
2. 隣接する要素が逆順であれば交換する
3. 終わりまで繰り返したら一番最後のデータがソート済みになる
4. 未ソートの部分がなくなるまで 1~3 を繰り返す

以下に C 言語での実装例を示します。

#include <stdio.h>
 
void bubbleSort(int *data, int n)
{
	int i, j;
	for (i = 1; i < n; i++)
	{
		for (j = 0; j < i; j++)
		{
			if (data[j] < data[j+1])
			{
				int tmp = data[j];
				data[j] = data[j+1];
				data[j+1] = tmp;
			}
		}
	}
}

バブルソートの計算量

今回はバブルソートのデータ比較回数について着目し、計算量の議論を行います。

はじめにバブルソートは、はじめから終わりまで隣接したデータを比較するので、データ数$N$に対して、$N-1$回の比較を行うことになります。

次に、$N-1$回の比較を行った後、最大値が一番最後に来るので、次の$N-2$回の比較を行います。

このように、$N-1$回、$N-2$回、$N-3$回、$\cdots$、$1$回の比較を行うことになります。

これを数式で表すと、以下のようになります。

この式は等差数列としてみなすことができます。

等差数列の和の公式を用いると、以下のようになります。

この式は $N$ について 2 次の式になっているので、$O(N^2)$となります。

したがって、バブルソートの計算量は$O(N^2)$となります。