クイックソート実装・詳しい計算量解説

クイックソート(Quick Sort)

このサイトでのクイックソートの定義は以下の通りです。¹

計算量 $O(N \log N)$

クイックソートのアルゴリズム

クイックソートは、分割統治法を用いた効率的なソートアルゴリズムです。以下の手順で動作します。

1. 配列の中から一つの要素を「ピボット」として選択します。(このサイトでは配列の一番左をピボットとします。)
2. ピボットを基準にして、配列を「ピボットより小さい要素」と「ピボットより大きい要素」の二つのサブ配列に分割します。
3. サブ配列に対して再帰的にクイックソートを適用します。

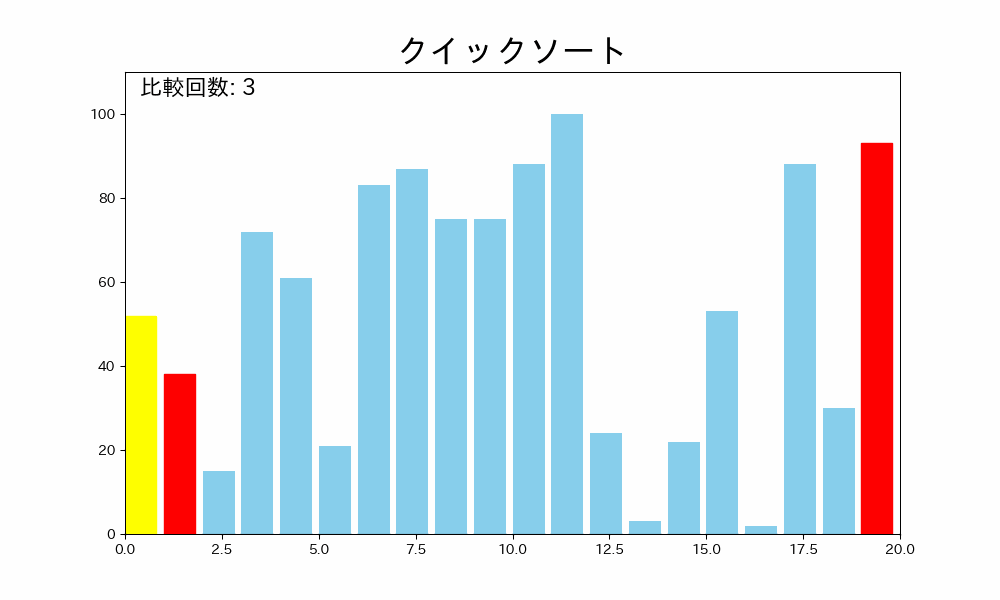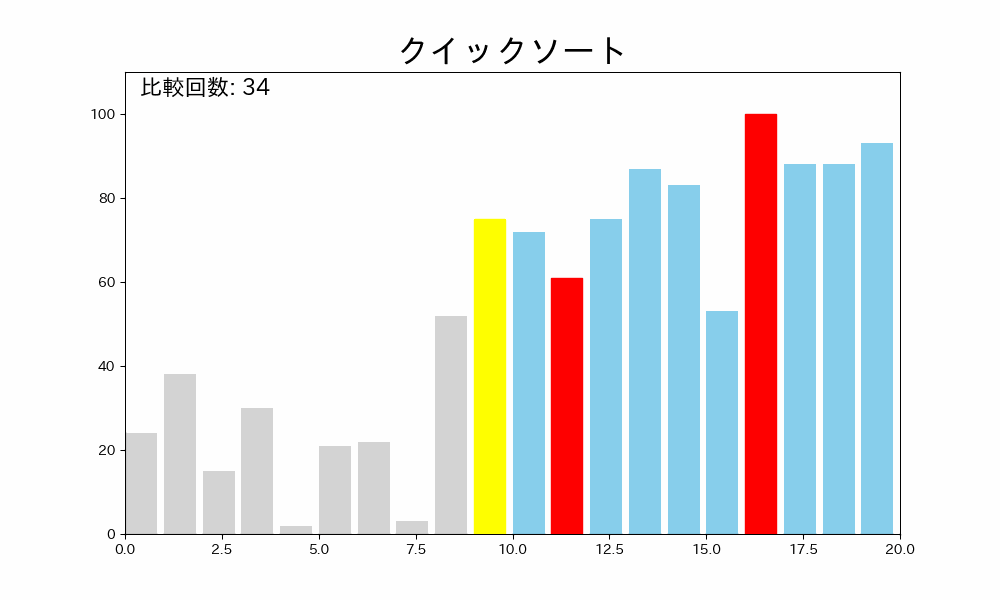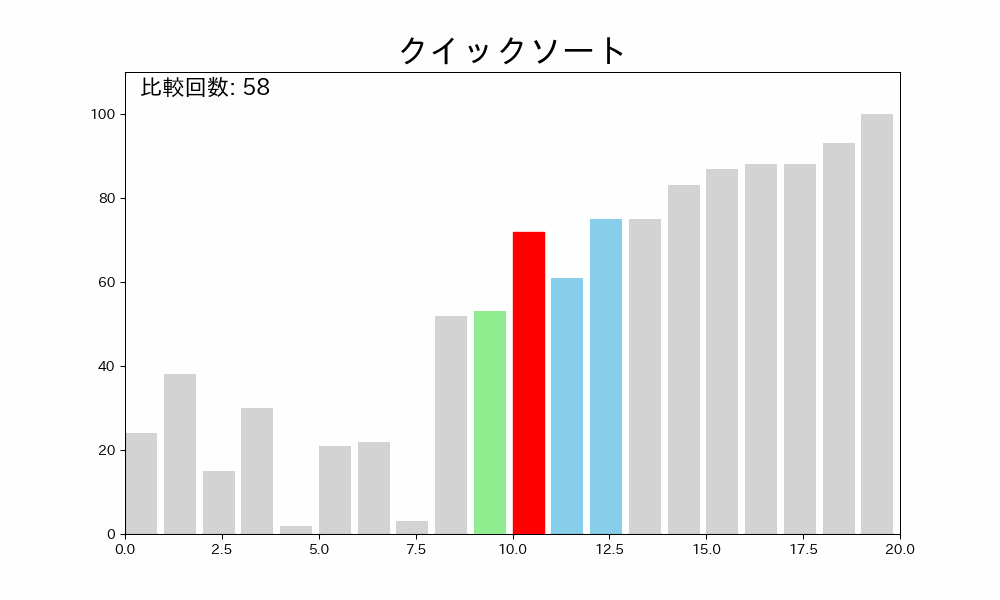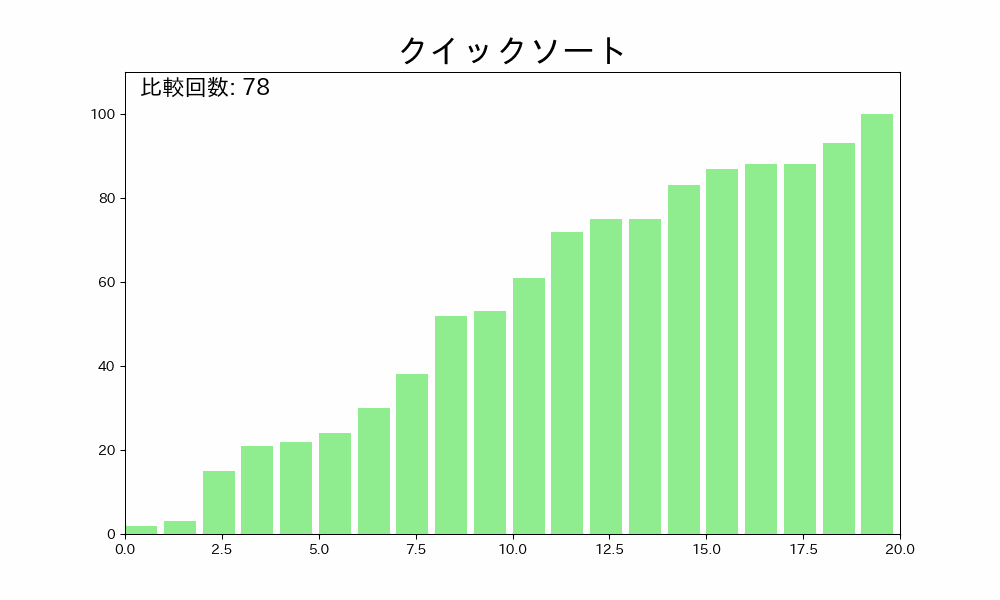
これを繰り返すことで、配列が整列されます。

2. サブ配列に分割

ピボットを除いた、配列の左端を i、右端を j とします。

• i のデータがピボットより小さい間、i を増加させます。
• j のデータがピボットより大きい間、j を減少させます。
• 邪魔なデータがあり、止まったら i と j のデータを交換します。

これを繰り返すと、ピボットより小さい要素と大きい要素に分かれます。

つまり、そのサブ配列の間にピボットが入ることが確定できます。

3. 再帰的にソート

移動させたピボットの左右の分割されたサブ配列に対して、再帰的にクイックソートを適用します。

実装例

以下に C 言語での実装例を示します。

void quickSort(int *d, int left, int right) {
    if (left < right) {
        int pivot = d[left];
        int i = left + 1;
        int j = right;
 
        while (1) {
            while (i <= right && d[i] <= pivot) {
                i++;
            }
            while (j >= left + 1 && d[j] > pivot) {
                j--;
            }
            if (i > j) {
                break;
            }
            // ピボットより大きい要素と小さい要素に分かれるように邪魔なもの同士を交換
            int temp = d[i];
            d[i] = d[j];
            d[j] = temp;
        }
 
        // ピボットをサブ配列との間に移動
        d[left] = d[j];
        d[j] = pivot;
 
        // 再帰的にソート
        quickSort(d, left, j - 1);
        quickSort(d, j + 1, right);
    }
}

クイックソートの計算量

今回はクイックソートの平均計算量について議論します。

クイックソートは、配列を分割し、分割された部分を再帰的にソートするアルゴリズムです。

平均の比較回数について着目し、計算量の議論を行います。

平均計算量

クイックソートで、発生する比較回数を$Q(N)$とします。

クイックソートの比較回数はデータに依存するため、サブ配列を $a$ と $b$ に分割した場合、以下のような式が成り立ちます。

この式からすべてのケースを考慮し、平均値を求めると以下のような式が成り立ちます。

$N$個のこの式をすべて足して、$N$ で割ると以下のような式が成り立ちます。

この式を変形すると以下のようになります。(1)式

N が N-1 のとき以下 (2)式

(1)式を(2)式で引くと以下のようになります。

この式を整理すると以下のようになります。

$R(N) = \frac{Q(N)}{N+1}$ とおくと、以下のようになります。

よって$R(N)$は

この式に$N+1$をかけると$Q(N)$が求まります。

$\frac{1}{k}$の和は積分を求め、近似することで以下のようになります。

よって、クイックソートの平均計算量は以下のようになります。

したがって、クイックソートの平均計算量は $O(N \log N)$ となります。

クイックソートは、データの分布やピボットの選択方法によっては最悪計算量が $O(N^2)$ になる場合もありますが、一般的には非常に効率的なソートアルゴリズムとして広く利用されています。

クイックソートは、安定なソートではありませんが、インプレースソート（追加のメモリをほとんど使用しない）であり、大規模なデータセットに対しても高速に動作します。

以上がクイックソートの基本的な解説と C 言語での実装、および計算量の議論でした。

(補足)計算量における log の底について

ここからは計算量の議論についての補足です。

ここで、$\log$ の底について考えてみましょう。

計算量の議論では、$\log$ の底は基本的に問題になりません。

なぜなら、$\log$ の底が異なる場合でも、それは定数倍の違いに過ぎないためです。

例えば、$\log_2 N$ と $\log_{10} N$ では、$\log_{10} N = \frac{\log_2 N}{\log_2 10}$ となります。

$\log_2 10$ は定数なので、$\log_2 N$ と $\log_{10} N$ の計算量は同じと考えることができます。