挿入ソート実装・詳しい計算量解説

挿入ソート(Insertion Sort)

このサイトでの挿入ソートの定義は以下の通りです。¹

計算量 $O(N^2)$

挿入ソートのアルゴリズム

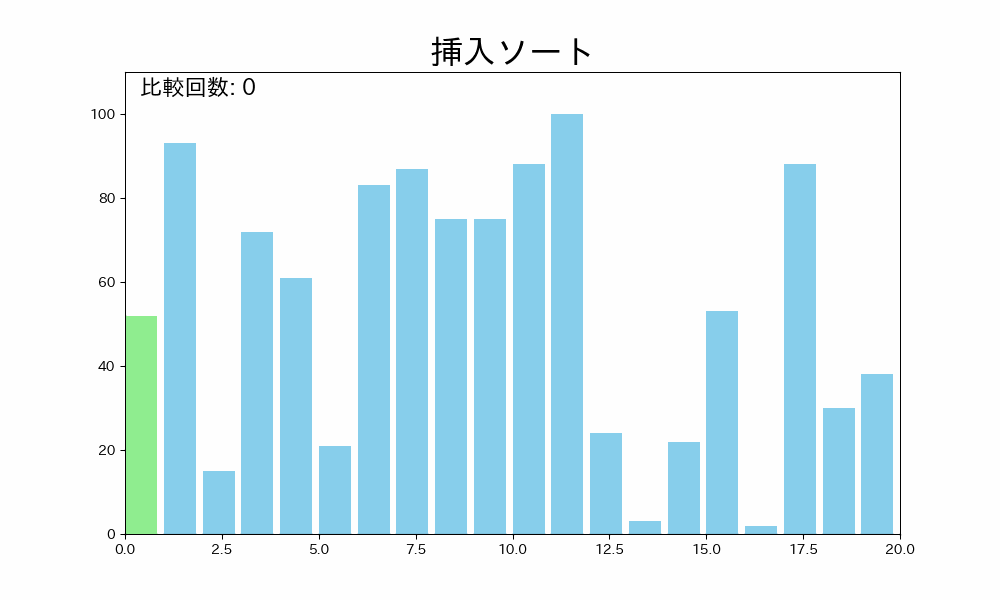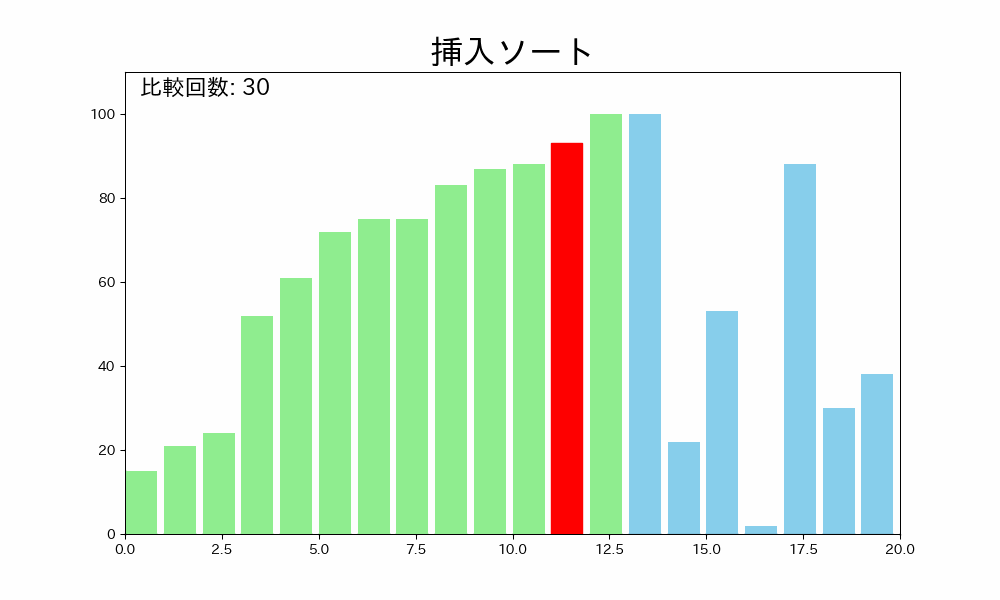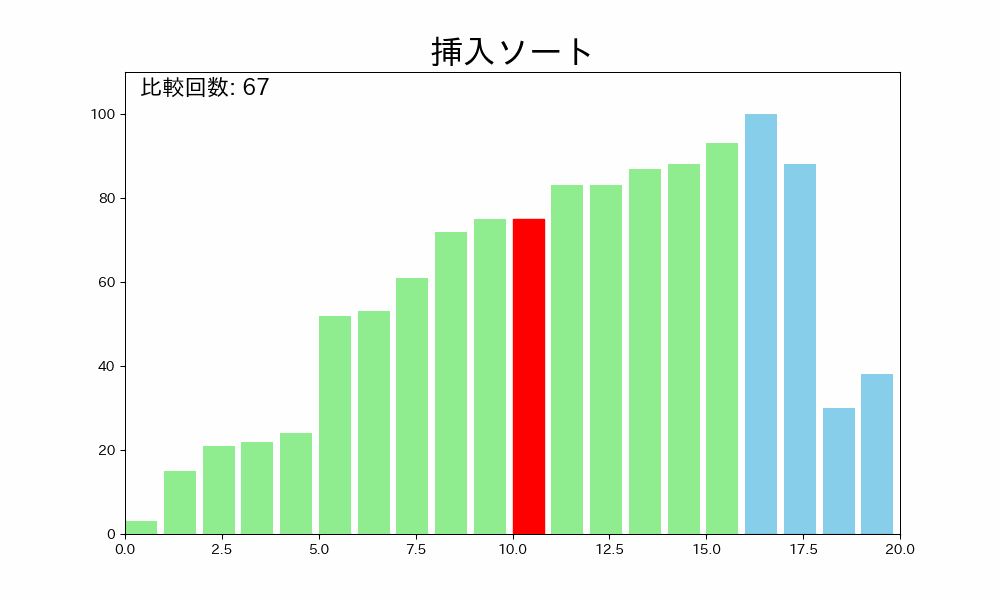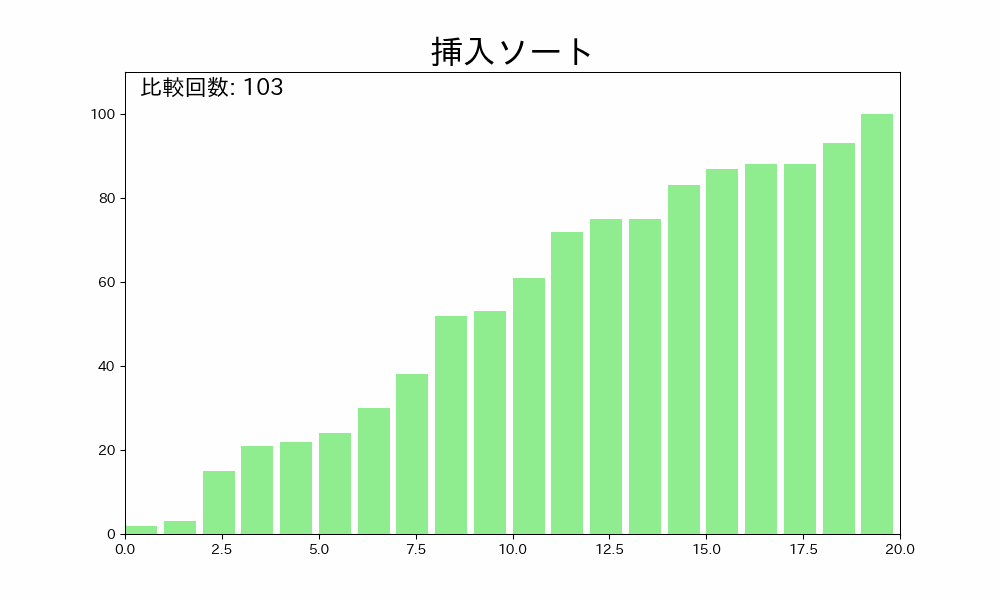
挿入ソートはデータ配列のはじめから終わりまで、ソート済みの部分と未ソートの部分に分け、未ソートの部分から一つずつ取り出して、ソート済みの部分に挿入していくアルゴリズムです。

詳しく手順を説明すると以下の通りです。

1. 未ソートの部分の先頭から要素を取り出す
2. ソート済みの部分の末尾から先頭に向かって、取り出した要素を挿入する場所を探す
3. 取り出した要素を挿入する場所を見つけたら、その場所に取り出した要素を挿入する
4. 未ソートの部分がなくなるまで 1~3 を繰り返す

以下に C 言語での実装例を示します。

void insertionSort(int *data, int n)
{
	int i, j;
	for (i = 1; i < n; i++)
	{
		if (data[i-1] > data[i])
		{
			int pick = data[i];
			for (j = i; j > 0 && data[j-1] > pick; j--)
			{
				data[j] = data[j-1];
			}
			data[j] = pick;
		}
	}
}

挿入ソートの計算量

今回は挿入ソートの最悪の場合のデータ比較回数について着目し、計算量の議論を行います。

挿入ソートの最悪の場合は、すべてデータが逆順に並んでいる場合です。

ソート済みの部分の末尾から先頭に向かって、取り出した要素を挿入する場所を探すため、データ比較回数がソート済みの部分の数になります。

よって、データを挿入するごとに、$1, 2, 3, \cdots, N-1$回のデータ比較が必要になります。

この場合、データ比較回数は以下のようになります。

等差数列の和の公式を用いて変形します。

よって、挿入ソートの最悪の場合の計算量は$O(N^2)$となります。