シェーカーソート実装・詳しい計算量解説

シェーカーソート(Cocktail Shaker Sort)

このサイトでのシェーカーソートの定義は以下の通りです。¹

計算量 $O(N^2)$

シェーカーソートのアルゴリズム

シェーカーソートはバブルソートの変形であり、データ配列を両方向に交互にバブルソートを行うアルゴリズムです。バブルソートが片方向にしかデータを移動しないのに対し、シェーカーソートは前方と後方の両方向にデータを移動させます。

バブルソートの詳しい解説はこちらを参照してください。

バブルソート実装・詳しい計算量解説

バブルソート(Bubble Sort)の説明、C言語での実装、数式を用いた計算量の議論を解説します。 計算量、比較回数、交換回数等々を用いて途中式まで解説。 バブルソートは一番簡単と言われるソートアルゴリズムです。 計算量はO(N^2)です。

blog.taiyaki.cc

詳しく手順を説明すると以下の通りです。

1. 配列の最初から最後まで隣接する要素を比較し、順序が逆の場合は交換する（前方走査）
2. 最後に到達したら、方向を逆にして、配列の最後から最初まで同様に隣接する要素を比較し、順序が逆の場合は交換する（後方走査）
3. ソートが完了するまで 1 と 2 を繰り返す

注: 最後に交換が行われた位置を記録し、次の走査の範囲を狭めることで、ソートの効率を向上させることができます。

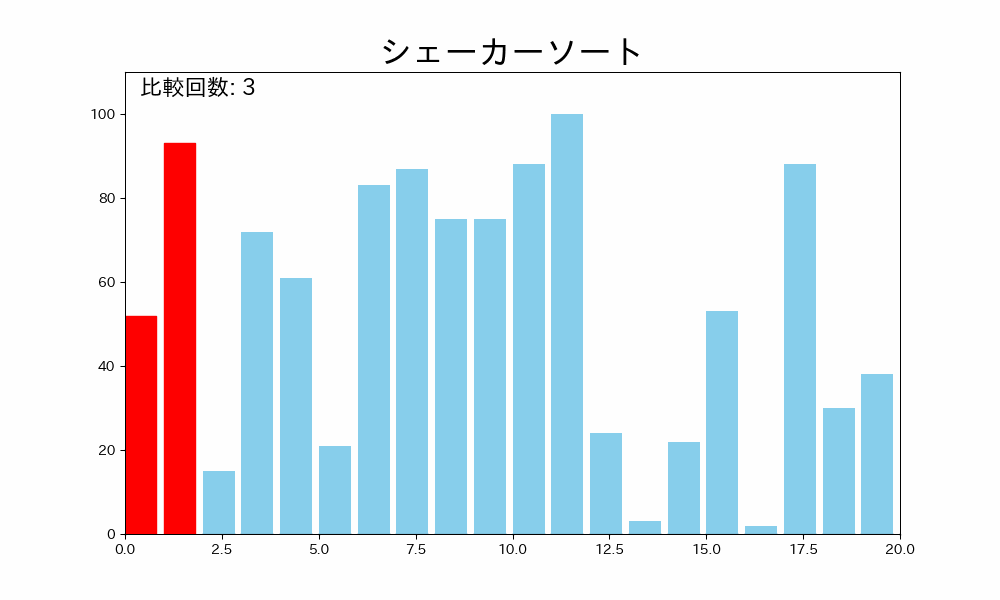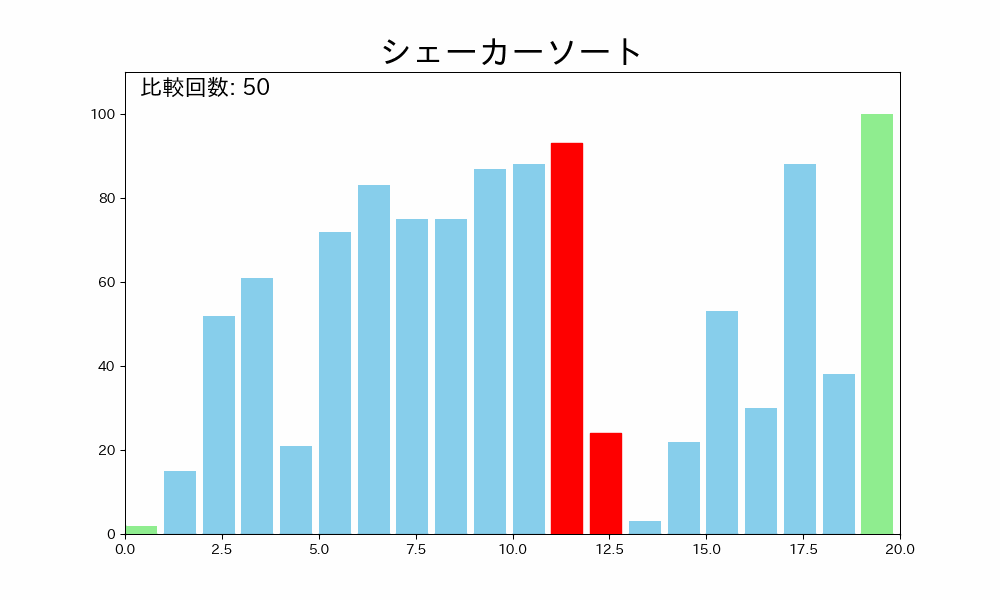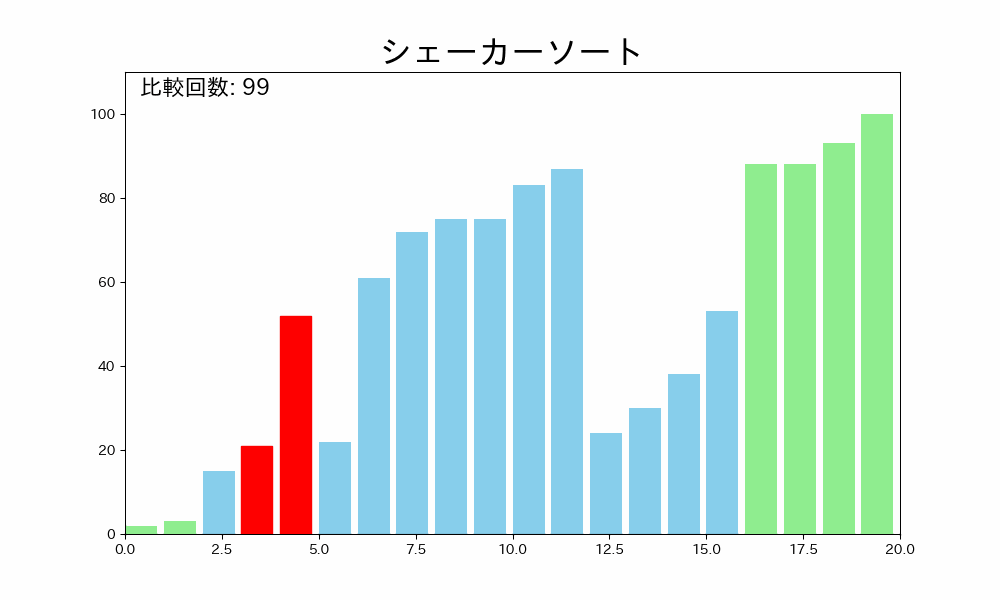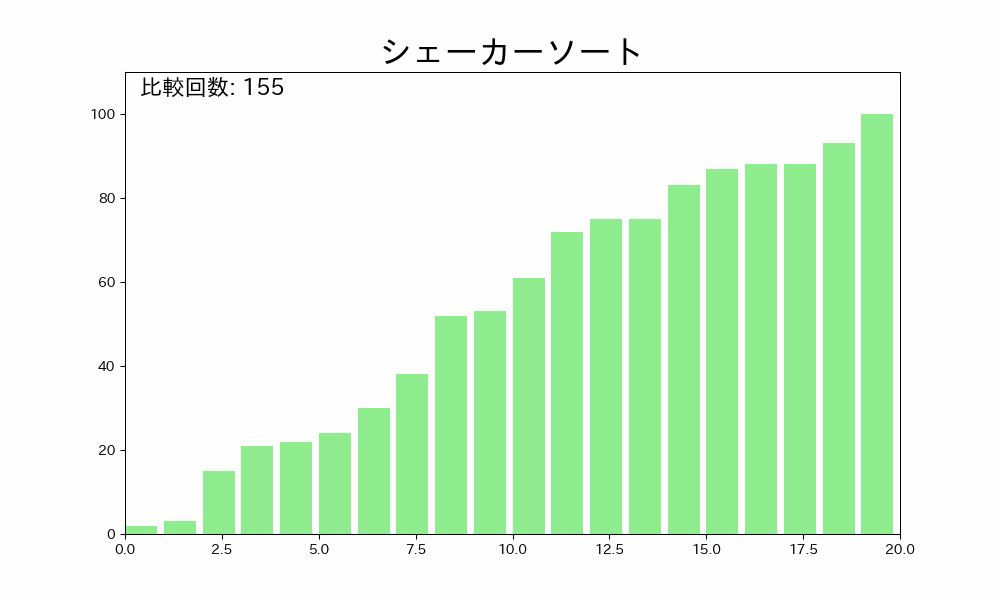
以下に C 言語での実装例を示します。

void shakerSort(int *data, int n)
{
    int i, left = 0, right = n - 1, last;
    while (left < right)
    {
        last = left;
        for (i = left; i < right; i++)
        {
            if (data[i] > data[i + 1])
            {
                int temp = data[i];
                data[i] = data[i + 1];
                data[i + 1] = temp;
                last = i;
            }
        }
        right = last;
        for (i = right; i > left; i--)
        {
            if (data[i - 1] > data[i])
            {
                int temp = data[i];
                data[i] = data[i - 1];
                data[i - 1] = temp;
                last = i;
            }
        }
        left = last;
    }
}

シェーカーソートの計算量

今回はシェーカーソートの平均計算量について着目し、計算量の議論を行います。

シェーカーソートは、前方と後方のソートを交互に行うため、各操作でのデータ比較と交換が行われます。

まず、右向きまたは左向きのバブルソートを行った際に、データ比較回数が通常より $x$ 回削減されるものとして議論します。

最初に data[0] から data[N-1] に向けて右方向へバブルソートを行うことから考えます。この時、隣接するデータを比較する回数は $(N-1)-x$ 回です。

同様に考えていくとソートが完了するまでのバブルソートの回数は、以下のようになります。

この時、データ比較回数は以下のようになります。

この式は厳密性に欠けるが、計算量の議論は続けて議論します。

$n$ の式は $N$ の一次式であるため、この式の右辺は一項、二項ともに $N$ の二次式である。

よってシェーカーソートの計算量は平均的に $O(N^2)$ であると言えます。

シェーカーソートはデータの順序がほぼ整っている場合や、逆順に近い場合ではバブルソートよりも効率的に動作することがありますが、基本的には計算量が $O(N^2)$ であるため、大規模なデータセットに対しては効率が良いとは言えません。